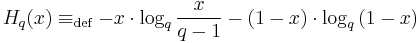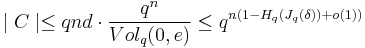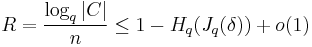Elias Bassalygo bound
The Elias-Bassalygo bound is a mathematical limit used in coding theory for error correction during data transmission or communications. The properties of the Elias-Bassalygo bound are defined, below, using mathematical expressions.
Contents |
Definition
Let  be a
be a  -ary code of length
-ary code of length  , i.e. a subset of
, i.e. a subset of ![[q]^n](/2012-wikipedia_en_all_nopic_01_2012/I/fd56f53f413fd36b409cfdc732be355d.png) . (Each
. (Each  -ary block code of length
-ary block code of length  is a subset of the strings of
is a subset of the strings of  where the alphabet set
where the alphabet set 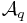 has
has  elements). Let
elements). Let  be the rate of
be the rate of  and
and  (delta) be the relative distance.
(delta) be the relative distance.
Let ![B_q(\boldsymbol{y}, \rho n) =\{ \boldsymbol{x} \in [q]^n | \Delta(\boldsymbol{x}, \boldsymbol{y}) \le \rho n \}](/2012-wikipedia_en_all_nopic_01_2012/I/36f4e8149f4944dab727354ba94bb172.png) be the Hamming ball of radius
be the Hamming ball of radius 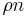 centered at
centered at 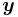 . Let
. Let 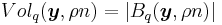 be the volume of the Hamming ball of radius
be the volume of the Hamming ball of radius 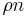 . It is obvious that the volume of a Hamming Ball is translation-invariant, i.e. irrelevant with position of
. It is obvious that the volume of a Hamming Ball is translation-invariant, i.e. irrelevant with position of 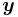 . In particular,
. In particular, 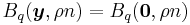 .
.
With large enough  , the rate
, the rate  and the relative distance
and the relative distance  satisfies the Elias-Bassalygo bound:
satisfies the Elias-Bassalygo bound: 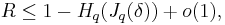
where
is the q-ary entropy function and
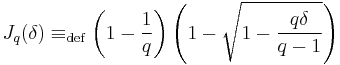 is a function related with Johnson bound.
is a function related with Johnson bound.
Proof
To prove the Elias–Bassalygo bound, start with the following Lemma:
Lemma 1: Given a q-ary code, ![C\subseteq [q]^n](/2012-wikipedia_en_all_nopic_01_2012/I/85eac2353e9987c83c520fed5b7a0f6a.png) and
and 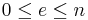 , there exists a Hamming ball of radius
, there exists a Hamming ball of radius  with at least
with at least 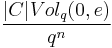 codewords in it.
codewords in it.
Proof of Lemma 1: To prove Lemma 1, use the probability method. Randomly pick a received word ![y \in [q]^n](/2012-wikipedia_en_all_nopic_01_2012/I/3f216e041cf866c4468452a80a8265b3.png) . The expected size of overlapped region between
. The expected size of overlapped region between  and the Hamming ball centered at
and the Hamming ball centered at  with radius
with radius  ,
, 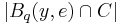 is
is 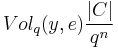 since
since  is (uniform) randomly selected. Since this is the expected value of the size, there must exist at least one
is (uniform) randomly selected. Since this is the expected value of the size, there must exist at least one  such that
such that 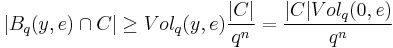 , otherwise the expectation must be smaller than this value.
, otherwise the expectation must be smaller than this value.
Now we prove the Elias–Bassalygo bound.
Define 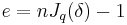 .
.
By Lemma 1, there exists a Hamming ball with  codewords such that
codewords such that 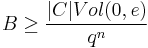
By the Johnson bound, we have 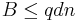 . Thus,
. Thus,
The second inequality follows from lower bound on the volume of a Hamming ball: 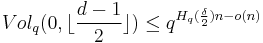 .
.
Putting in 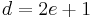 and
and 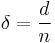 gives the second inequality.
gives the second inequality.
Therefore we have
See also
References
Bassalygo, L. A. (1965), "New upper boundes for error-correcting codes", Problems of Information Transmission 1 (1): 32–35
Claude E. Shannon, Robert G. Gallager; Berlekamp, Elwyn R. (1967), "Lower bounds to error probability for coding on discrete memoryless channels. Part I.", Information and Control 10: 65–103
Claude E. Shannon, Robert G. Gallager; Berlekamp, Elwyn R. (1967), "Lower bounds to error probability for coding on discrete memoryless channels. Part II.", Information and Control 10: 522–552